derivadas parciales

Las matemáticas

Antes de hablar de las derivadas parciales, tenemos que empezar hablando de las matemáticas. La matemática es la ciencia de la estructura, el orden y los patrones repetitivos que se basa en contar, medir y describir las formas. Su objetivo de estudio son las magnitudes, las cantidades y los cambios de estas en el tiempo y el espacio.

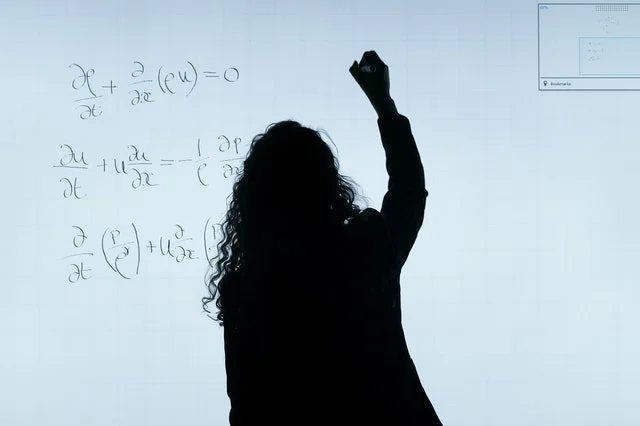
Te has preguntado alguna vez, ¿Qué estudia las matemáticas?. Aunque las matemáticas tratan de muchos aspectos. Hay una nueva demanda de matemáticos en muchos campos de la industria y los negocios, no sólo en la ciencia. Las matemáticas estudia:

• Los números.
• Estructuras, formas y construcciones geométricas.
• Juegos.
• probabilidades.
• Acertijos y enigmas.
• Patrones y sucesiones. 

Ramas de las matemáticas

Por un lado, las matemáticas podrían dividirse en dos grandes áreas:

• Matemática pura: estudia los métodos, para determinar de forma lógica cuáles de estos métodos son correctos.
• Matemática aplicada: es el uso de la matemática para resolver problemas de la vida real.

Por otro lado, podemos también clasificar la matemática en diferentes ramas, a saber:

• Aritmética: es el estudio de los números reales, aquellos que usamos para contar. La aritmética es esencial para cualquier profesión. Sumas, restas, multiplicación, división, fracciones y otros más son elementos de la aritmética.
• Álgebra: estudia la cantidad de un modo general. Para esto, se vale de números y letras para representar las fórmulas algebraicas, por ejemplo, y=2ax+3b.
• Cálculo: es la rama de la matemática involucrado con los cambios. Aquí entran las derivadas y las integrales, entre otros conceptos. 
• Geometría: estudia las dimensiones y las formas de los objetos. 
• Teoría de juegos: es la rama más moderna de la matemática, pero no trata de juegos, como ajedrez o damas. Trata si de la toma de decisiones.
• Probabilidades: la teoría de probabilidades nos dice como determinar que un evento pueda ocurrir. En todos los campos de la ciencia se utiliza la estimación de probabilidades. Una cirugía o un tratamiento médico tiene cierta posibilidad de ser exitoso, lo que determina que tan seguro es ese procedimiento. Los asesores políticos miden las probabilidades de ganar las elecciones de un cierto partido.
• Estadística: esta rama de la matemática se encarga de la colección de datos, su organización, análisis e interpretación.

¿Cuáles son los pasos a seguir a la hora de resolver derivadas parciales?

Las matemáticas es una de las asignaturas que, para quien no logre entenderlas, supone un gran esfuerzo por comprender las múltiples y complejas operaciones que se deben de desarrollar. En un nivel más avanzado, por ejemplo de instituto, los alumnos deben de llevar a cabo operaciones que se alejan de la suma y la resta. Este es el caso de las derivadas. Las derivadas son operaciones matemáticas que tienen como objetivo determinar cómo cambia el valor de una función, a medida que va cambiando el valor de la variable independiente incluida en la misma. 

La derivada también se puede definir como la pendiente de la recta que se encuentra en posición tangente a la gráfica en el punto de la función del que se hable. La operación necesaria para hallar el resultado puede ser sencilla. Sin embargo, la complejidad aumenta cuando en la función se puede encontrar más de una variable independiente, en cuyo caso será necesario fraccionar la operación por partes, dando lugar a las derivadas parciales. 

Para simplificar el cálculo, lo ideal es ir resolviendo las variables, haciendo la derivada, dejando el resto constantes. La necesidad de realizar la derivada por partes es el motivo por el cual se denomina derivadas parciales.

Descubre la aplicación de las derivadas parciales a problemas de optimización

Muchos de los problemas que se presentan en la práctica diariamente, están relacionados de una forma u otra, con encontrar los valores máximos y mínimos de una función, y más aún, determinar par qué valores de la variable independiente se alcanzan estos. Estos problemas se llaman de forma genérica: problemas de optimización.

En términos generales, un problema de optimización consiste  en encontrar el valor mínimo o minimizar o encontrar el valor máximo o maximizar, una cierta función, de tal forma que satisfagan ciertas condiciones dadas.

Las soluciones optimas son aquellas para las cuales se satisfacen las restricción del problema y el valor de la función sea máximo o mínimo. La función que representa el problema de optimización se le llama función objetivos. Las fases en la solución de un problema de optimización son las siguientes:

• Planteamiento del problema.
• Formulación matemática, se trata de construir la función objetivo si no se da explícitamente.
• Análisis del comportamiento de la función objetivo que puede incluir su representación gráfica.
• Obtención de las soluciones.

¿En qué ámbitos empleamos las derivadas parciales?

Las aplicaciones de las derivadas parciales pueden englobar más ámbitos aparte de como es lógico, las matemáticas. Sino que también se usan mucho en el ámbito de la economía, el concepto de derivada parcial hace referencia a la marginalidad. De esta manera a partir de una función de coste podemos obtener la función de coste marginal respecto de una u otra variable. Análogamente también podríamos hallar la producción marginal o análisis marginal.

Además también se utiliza la derivada parcial en física para expresión la ecuación  de difusión del calor.

En el área de estudios de Ecuaciones derivadas parciales  disponemos de un  un gran abanico de estudios como también de salidas profesionales.

Una derivada tiene como una de sus funciones una variable mantenido otra variable constante. Hay más conceptos importantes como integral indefinida, integral definida o integral de sucesión. En este curso habrá ejercicios que puedes hacer para que aprendas todo sobre la derivada. y por último, los ejercicios constarán en saber derivar, aplicar bien cada regla de derivación respecto a cada variable y saber hace un cálculo con la calculadora sin dar feedback.

Si quieres saber más sobre derivadas parciales. Ya puedes apuntarte a nuestros cursos online. ¡Descúbrelos de la mano de Euroinnova!.