Índice
Entender la ley de los signos matemáticos desde el principio evita la mayoría de errores al operar números con signo en secundaria, bachillerato y cursos de ingreso universitario.
Así pues, esta es una regla que resume cómo se comportan los signos (+ y –) en suma, resta, multiplicación y división. Dominarla te ahorra tiempo, te ayuda a comprobar resultados con rapidez y prepara el terreno para álgebra, ecuaciones y funciones.
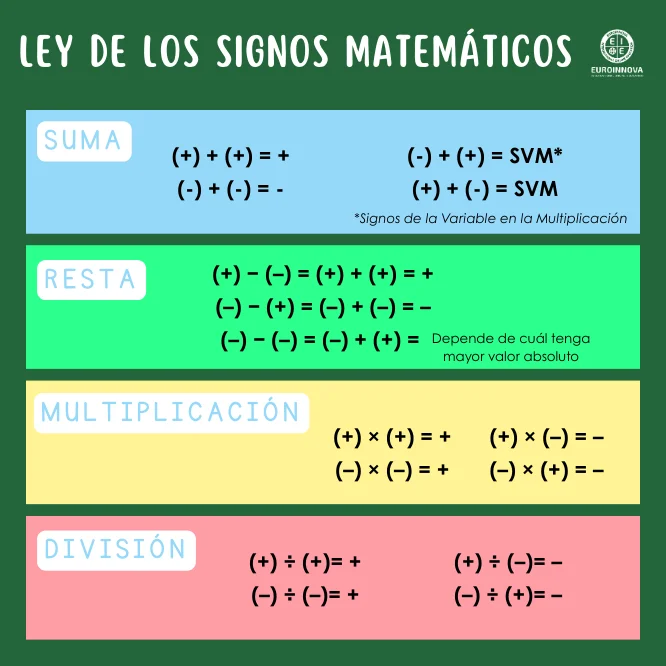
La ley de los signos de la suma se basa en que, al sumar números con el mismo signo, se suman los valores absolutos y se conserva el signo común, mientras que, al sumar números con signos distintos, se restan los valores absolutos y el resultado adopta el signo del número de mayor valor absoluto.
Esto se alinea con la interpretación en la recta numérica, de manera que, es posible avanzar a la derecha (positivo) o a la izquierda (negativo) según la magnitud dominante.
Además, en materiales de aula se trabajan ejercicios graduados de suma y resta de positivos y negativos para reforzar el razonamiento con valores absolutos.
De esta forma, algunos ejemplos rápidos son los siguientes:
En lo que respecta a la ley de los signos de la resta, hay que recordar que restar es sumar el opuesto: a – b = a + (–b). De esa forma, la resta hereda la regla de la suma.
Asimismo, cambia el segundo número por su opuesto y aplica la estrategia anterior.
Ejemplos:
En la ley de los signos en la multiplicación, los signos iguales dan positivo, mientras que, los signos distintos dan negativo. Por lo tanto, multiplicar implica sumar repetidamente, y la consistencia de signos se puede justificar con propiedades de los enteros.
Ejemplos:
La lógica de la ley de los signos en la división es exactamente la misma que en la multiplicación, es decir, que, los signos iguales producen positivo y los signos distintos producen negativo. También es importante cuidar el tratamiento del cero, de manera que, dividir entre 0 no está definido.
Ejemplos:
Los principales errores en el uso de la ley de los signos en matemáticas son los siguientes:
Un desliz frecuente es “cruzar” reglas: aplicar la tabla de multiplicación/división a una suma/resta.
Si ves un símbolo “+” o “–” entre números sin paréntesis que indiquen producto, estás en suma o resta. Aplica el criterio de valores absolutos y signo dominante, no la tabla de productos.
Otro error típico es pensar que (–) × (–) resulta negativo. Refuerza la regla con patrones: (–2) × (+3) = –6; (–2) × (+2) = –4; (–2) × (+1) = –2; (–2) × 0 = 0; si sigues restando 2 al resultado al disminuir el factor positivo, al pasar de +1 a 0 a –1, el patrón obliga a (–2) × (–1) = +2, y así sucesivamente.
En definitiva, se tiene que interpretar el signo como dirección, utilizar el valor absoluto para decidir “quién domina” en suma/resta y respetar la tabla de signos en productos y cocientes. Con ese marco, cualquier problema que involucre enteros, se vuelve más transparente y controlable.
A continuación, presentamos 4 ejercicios resueltos de la ley de los signos:
Calcula: (–18) + (+25) + (–7).
Solución paso a paso: agrupa positivos y negativos.
Suma positivos: 25.
Suma negativos: –25 (–18 –7).
Resultado: 25 + (–25) = 0.
Calcula: (–12) – [ (–9) – (+5) ].
Solución: primero resuelve el corchete: (–9) – (+5) = –14. Luego: (–12) – (–14) = –12 + 14 = +2.
Calcula: (–6) × (+4) × (–3).
Solución: multiplica por partes: (–6) × (+4) = –24; luego (–24) × (–3) = +72 (2 signos negativos en total → resultado positivo).
Calcula: [ (–56) ÷ (–7) ] ÷ (+2).
Solución: (–56) ÷ (–7) = +8; luego +8 ÷ (+2) = +4.
Algunas de las aplicaciones de la ley de los signos matemáticos son las siguientes:
En finanzas personales básicas y en problemas escolares, los positivos representan ingresos/ganancias y los negativos, egresos/deudas.
Ejemplo: saldo del día = saldo anterior + ingresos – egresos. Si debes $120 (–120) y recibes $80 (+80), tu saldo es –40: sigues debiendo, pero menos. Con varias transacciones, agrupa por signo y aplica las reglas descritas antes; de esa manera, reduces errores de cálculo y justificas el resultado con claridad.
Moverse en el plano exige sumar o restar desplazamientos con signo: avanzar a la derecha/arriba (+) o a la izquierda/abajo (–). Si partes de (–3, 2) y aplicas el vector (+5, –7), llegas a (2, –5) porque –3 + 5 = 2 y 2 + (–7) = –5. Este mismo razonamiento se usa en física básica (desplazamientos) y en programación de gráficos.
De tal manera, en los programas y materiales educativos oficiales, las operaciones con números enteros se suelen estudiar de una manera progresiva con el apoyo de la recta numérica, así como de tablas de signos.
Al respecto, es conveniente proponer actividades para visualizar sumas y restas de enteros en la recta numérica y consolidar el sentido de dirección y magnitud del movimiento.
Dominar la ley de los signos te da seguridad para resolver desde sumas y restas cotidianas hasta problemas de álgebra, física y finanzas.
Así pues, es aconsejable practicar con la recta numérica, al igual que, verificar multiplicaciones y divisiones con la tabla de signos, comprobando cada resultado con una lectura de magnitud y dirección.
Quizá te interesa leer sobre:


¡Muchas gracias!
Hemos recibido correctamente tus datos. En breve nos pondremos en contacto contigo.