Índice
Comprender y trazar figuras en el plano cartesiano con coordenadas fáciles es una de las habilidades que más rápido eleva el desempeño en geometría analítica a nivel escolar y universitario.
De tal forma, con un puñado de puntos enteros bien elegidos, es decir, pares ordenados (x,y)(x, y) sencillos, puedes construir triángulos, cuadriláteros y verificar sus propiedades sin cálculos complicados.
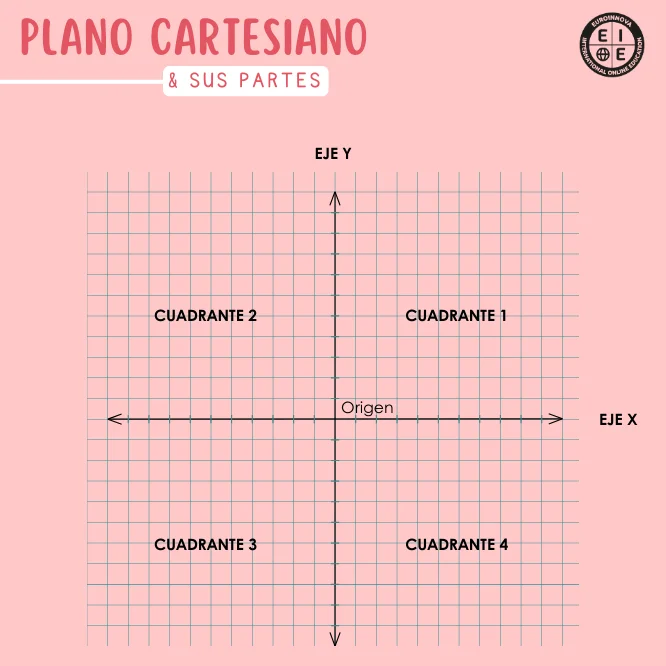
El plano cartesiano está formado por 2 ejes perpendiculares, los cuales son el eje horizontal de las abscisas (eje xx) y el eje vertical de las ordenadas (eje yy).
Ambos se cruzan en el origen (0,0)(0,0).
Para ubicar un punto (x,y)(x, y): primero te mueves xx unidades sobre el eje horizontal (a la derecha si x>0x>0, a la izquierda si x<0x<0); después, yy unidades sobre el eje vertical (arriba si y>0y>0, abajo si y<0y<0).
Por ejemplo, (3,2)(3,2) está 3 a la derecha y 2 arriba del origen, mientras que, en materiales oficiales, se refuerza este procedimiento con actividades de graficación y lectura de coordenadas, pidiendo identificar ejes, pares ordenados y ubicaciones básicas.
A continuación, proponemos puntos con coordenadas enteras pequeñas para dibujar cada figura.
Traza los puntos y únelos en el orden indicado (cerrando la figura al final). Si tu cuaderno usa cuadrícula, bastará con contar casillas.
Puntos: (0,0)(0,0), (4,0)(4,0), (2,3)(2,3).
Características: 3 lados, 3 vértices. Es un triángulo escaleno (las longitudes de los lados son diferentes). Si quieres un triángulo isósceles fácil, prueba (0,0)(0,0), (4,0)(4,0), (2,3)(2,3) y verifica que 2 lados sean iguales con la fórmula de distancia.
Puntos: (1,1)(1,1), (5,1)(5,1), (5,5)(5,5), (1,5)(1,5).
Características: 4 lados iguales y 4 ángulos rectos. Para comprobarlo, mide las longitudes entre vértices consecutivos (todas deben ser iguales) y confirma que los lados adyacentes sean perpendiculares (pendientes negativas recíprocas: m1⋅m2=−1m_1 \cdot m_2 = -1).
Puntos: (−2,0)(-2,0), (4,0)(4,0), (4,2)(4,2), (−2,2)(-2,2).
Características: lados opuestos iguales y paralelos, 4 ángulos rectos. Aquí verás 2 lados de longitud 6 y 2 de longitud 2.
Puntos: (0,0)(0,0), (6,0)(6,0), (4,2)(4,2), (2,2)(2,2).
Características: al menos un par de lados paralelos. En este ejemplo, las bases (0,0)(6,0)‾\overline{(0,0)(6,0)} y (2,2)(4,2)‾\overline{(2,2)(4,2)} son horizontales (misma yy), por lo tanto, paralelas.
Puntos: (0,2)(0,2), (2,0)(2,0), (0,−2)(0,-2), (−2,0)(-2,0).
Características: 4 lados iguales, diagonales perpendiculares, de modo que, las diagonales son los ejes xx y yy, que se cruzan en ángulo recto en el origen.
Puntos (construido con 2 vectores simples): (0,0)(0,0), (3,1)(3,1), (4,4)(4,4), (1,3)(1,3).
Características: ambos pares de lados opuestos son paralelos y de igual longitud. Observa que el vector (3,1)(3,1) se repite en lados opuestos y el vector (1,3)(1,3) también, lo que garantiza el paralelismo.
Verificar figuras en el plano cartesiano con coordenadas fáciles te evita confusiones y fortalece tu razonamiento espacial. Además, en evaluaciones o proyectos, se suele valorar que justifiques cada rasgo con un criterio objetivo.
Empieza por lo elemental, recorriendo la figura y cuenta cuántos vértices hay, los cuales deben coincidir con los puntos que graficaste, además de cuántos segmentos la delimitan. Si “sobran” o “faltan” puntos, quizá uniste en orden distinto.
La longitud de un lado entre A(x1,y1)A(x_1,y_1) y B(x2,y2)B(x_2,y_2) se calcula con AB‾=(x2−x1)2+(y2−y1)2\overline{AB} = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}.
Dibuja siguiendo el listado de vértices (por ejemplo, 1→2→3→4→1). Para chequear paralelismo, compara pendientes: en 2 puntos (x1,y1)(x_1,y_1) y (x2,y2)(x_2,y_2), la pendiente es m=y2−y1x2−x1m=\frac{y_2-y_1}{x_2-x_1}.
Lados paralelos tienen la misma pendiente; lados perpendiculares tienen pendientes negativas recíprocas. Si una pendiente es indefinida (segmento vertical), su paralelo también será vertical.
De igual forma, cuando trabajes con figuras en el plano cartesiano con coordenadas fáciles, procura escoger puntos con diferencias ∣x2−x1∣|x_2-x_1| y ∣y2−y1∣|y_2-y_1| pequeñas (1, 2, 3 o 4 unidades).
De esa manera, las cuentas son rápidas y la verificación, inmediata.
Las aplicaciones prácticas de figuras en el plano cartesiano con coordenadas fáciles son las siguientes:
Estas figuras en el plano cartesiano con coordenadas fáciles sirven para introducir perímetros, áreas y propiedades de paralelismo y ortogonalidad.
En materiales oficiales suelen abundar tareas que piden ubicar puntos y elaborar gráficas. Además, en los programas se indican metas como ubicar puntos en el primer cuadrante, lo que sienta bases para álgebra y física.
El pensamiento en coordenadas es fundamental para hojas de cálculo, gráficos estadísticos, CAD y programación de gráficos.
De tal manera, en entornos educativos, se suele trabajar desde gráficas de funciones lineales hasta bocetos de planos sencillos.
Dominar figuras en el plano cartesiano con coordenadas fáciles te da un atajo didáctico, dado que, con pocos puntos enteros puedes construir y verificar formas sólidas sin álgebra avanzada.
Por lo tanto, empieza por el plano, practica la ubicación de pares ordenados y valida longitudes y pendientes para confirmar propiedades. Además, si quieres profundizar contando con acompañamiento estructurado, en Euroinnova encontrarás el Curso de Cálculo Diferencial en el cual se introduce la representación en el plano y conceptos clave que se usan al trazar figuras y funciones.
Quizá te interesa leer sobre:


¡Muchas gracias!
Hemos recibido correctamente tus datos. En breve nos pondremos en contacto contigo.