Índice
Entender cómo se organizan las caras, vértices y aristas de un paralelepípedo es clave para dominar la geometría espacial que se enseña en escuelas y universidades de todo el mundo. Así pues, este es un sólido tridimensional con estructura muy regular, siendo muy útil para medir, modelar y resolver problemas de ingeniería, arquitectura o empaque.
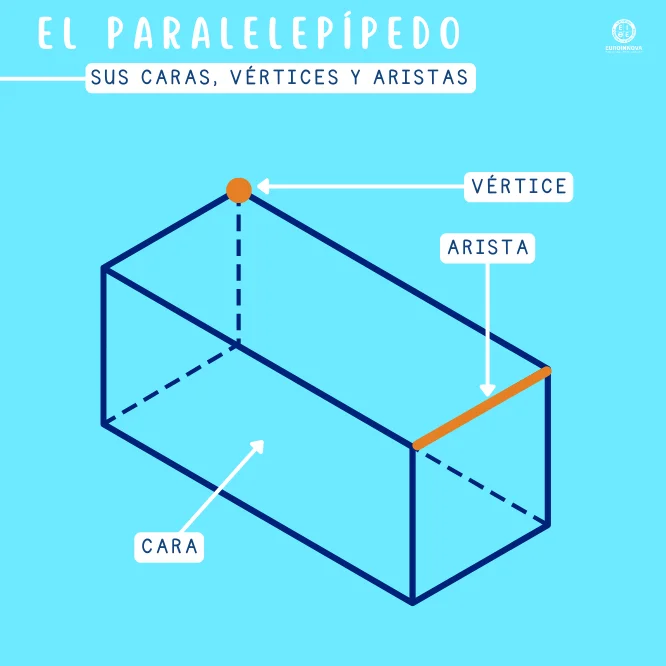
Un paralelepípedo es un prisma cuyas 6 caras son paralelogramos y en el que las caras opuestas son paralelas e iguales. De esta manera, si las 6 caras son rectángulos, estamos ante un paralelepípedo rectangular, que también es conocido como cuboide.
Asimismo, en matemáticas, su volumen general puede calcularse con el producto triple escalar de 3 aristas concurrentes en un vértice: V = |A · (B × C)|.
En lo que respecta a caras, vértices y aristas de un paralelepípedo, las caras se tratan de los paralelogramos que cierran el sólido. Todo paralelepípedo tiene 6 caras, agrupadas en 3 pares de caras opuestas y paralelas.
En la variante rectangular, cada cara es un rectángulo, siendo el caso más frecuente en cajas, ladrillos o bloques de concreto.
De esta forma, el trabajo con prismas rectos fomenta la identificación de sus caras y cómo el polígono de la base determina el nombre del prisma.
La forma de cómo identificarlas en la práctica consiste en imaginar una caja de cartón estándar. Hay que colocarla sobre una mesa, de modo que, la cara de abajo es la base; la cara de arriba es la tapa, mientras que, hay 4 caras laterales a los lados.
Si la despliegas, es decir, desarmas las pestañas, obtienes un desarrollo plano con 6 rectángulos. Esa vista plana es útil para calcular áreas de material, planear impresiones o verificar si el diseño cabe en una lámina, mientras que, en contextos de logística, suele tratarse de un ejercicio que ayuda a optimizar el uso de cartón y reducir mermas.
Con respecto a las caras, vértices y aristas de un paralelepípedo, los vértices son los puntos donde convergen 3 aristas. En cualquier paralelepípedo hay 8 vértices, es decir, 4 arriba y 4 abajo, los cuales están alineados de un modo en el que cada uno corresponde con el de la cara opuesta.
Esta simetría permite enumerarlos y ubicarlos con coordenadas sencillas, tales como, por ejemplo, usando sistemas x, y, z.
Por su parte, el modelado con coordenadas se trata de que, si sitúas un vértice en el origen (0,0,0) y haces que las 3 aristas incidentes tengan longitudes a, b y c alineadas con los ejes, los 8 vértices quedan en los puntos (0,0,0), (a,0,0), (0,b,0), (0,0,c), (a,b,0), (a,0,c), (0,b,c) y (a,b,c).
Este esquema es estándar en CAD y facilita medir distancias y diagonales. Si el paralelepípedo no es rectangular, el procedimiento es similar, pero sustituyes a, b, c por 3 vectores no coplanarios.
En lo concerniente a caras, vértices y aristas de un paralelepípedo, las aristas son los segmentos que unen los vértices y, además, delimitan las caras. Un paralelepípedo tiene 12 aristas, organizadas en 3 familias de aristas paralelas entre sí (4 por dirección).
En el caso rectangular, esas 3 direcciones suelen representarse con longitudes a, b y c, lo que facilita el cálculo de medidas.
Con relación a paralelismo y ortogonalidad, en el paralelepípedo rectangular, las 3 familias de aristas del paralelepípedo son mutuamente perpendiculares, mientras que, en el paralelepípedo oblicuo, las familias siguen siendo paralelas entre sí, pero forman ángulos oblicuos.
Este detalle importa al estimar esfuerzos en estructuras o al cortar materiales con sierras que solamente admiten cortes a 90°. En diseño asistido por computadora, fijar correctamente estas direcciones evita errores de ensamblaje y colisiones entre piezas.
Aparte de contar el número de caras, vértices y aristas de un paralelepípedo, conviene exponer algunas fórmulas prácticas y ver un ejemplo numérico:
Volumen general de un paralelepípedo cualquiera: V=∣A⋅(B×C)∣V = |\mathbf{A} \cdot (\mathbf{B} \times \mathbf{C})|. Esta expresión describe el paralelepípedo generado por 3 vectores y equivale al valor absoluto del determinante formado por sus componentes.
Volumen del paralelepípedo rectangular: V=a b cV = a\,b\,c, donde a, b y c son las longitudes de las aristas concurrentes en un vértice.
Área total del paralelepípedo rectangular: S=2(ab+bc+ac)S = 2(ab + bc + ac).
Diagonal espacial rectangular: d=a2+b2+c2d = \sqrt{a^2 + b^2 + c^2}.
Ejemplo: Supón un paquete con a = 40 cm, b = 25 cm y c = 18 cm. Entonces:
Volumen: V=40×25×18=18 000 cm3V = 40 \times 25 \times 18 = 18\,000\ \text{cm}^3 (18 litros).
Área total: S=2(40⋅25+25⋅18+40⋅18)=2(1000+450+720)=4 340 cm2S = 2(40\cdot25 + 25\cdot18 + 40\cdot18) = 2(1000 + 450 + 720) = 4\,340\ \text{cm}^2. Esta cifra te orienta sobre cuánta lámina de cartón mínimo necesitas, sin contar solapas.
Diagonal: d=402+252+182≈1600+625+324=2549≈50.5 cmd = \sqrt{40^2 + 25^2 + 18^2} \approx \sqrt{1600 + 625 + 324} = \sqrt{2549} \approx 50.5\ \text{cm}. Útil para verificar si cabe por una apertura diagonal.
Algunas buenas prácticas de comprobación cuando armes un modelo o resuelvas un problema son las siguientes:
Verifica que cuentas 6 caras, 12 aristas y 8 vértices.
Comprueba unidades (cm, m, in) antes de multiplicar.
Si cambias a un paralelepípedo oblicuo, usa el producto triple escalar y, si es posible, dibuja un esquema con los 3 vectores para evitar errores de signo.
Una fórmula para recordar las caras, vértices y aristas de un paralelepípedo consiste en memorizar este 3 en raya del paralelepípedo, es decir, 8 vértices, 12 aristas, 6 caras.
Si trabajas con modelos físicos (cajas, bloques o impresiones 3D), comprobarlo es inmediato. Para ello, cuenta los puntos (vértices), recorre los segmentos (aristas) y enumera las superficies planas (caras).
La relación de Euler afirma que, en todo poliedro convexo, el número de vértices (V) menos el número de aristas (A) más el número de caras (C) es igual a 2.
Para un paralelepípedo: V−A+C=8−12+6=2V - A + C = 8 - 12 + 6 = 2. Esta identidad no es una curiosidad, sino que, sirve para verificar conteos y detectar errores al modelar sólidos. Este es un resultado clásico de la topología y la geometría de poliedros con demostraciones disponibles.
Es crucial saber cómo medir, estimar o enseñar las caras, vértices y aristas de un paralelepípedo, el cual es una figura geométrica que, a pesar de su sencillez en apariencia, reúne propiedades claras y aplicables tanto en el ámbito académico como en situaciones prácticas de la vida cotidiana.
Así pues, su estructura, que se basa en la combinación de rectángulos y paralelogramos, lo convierte en un excelente ejemplo de cómo la geometría simple puede ofrecer soluciones concretas y funcionales, de manera que, comprender sus características no solamente fortalece la base matemática, sino que, también abre la puerta a un razonamiento más lógico y estructurado, fundamental para el aprendizaje y la aplicación de las ciencias exactas.
Quizá te interesa leer sobre:


¡Muchas gracias!
Hemos recibido correctamente tus datos. En breve nos pondremos en contacto contigo.